Stem-and-Leaf Plots
Purplemath
Stem-and-leaf plots are a method for showing the frequency with which certain classes of values occur. You could make a frequency distribution table or a histogram for the values, or you can use a stem-and-leaf plot and let the numbers themselves to show pretty much the same information.
For instance, suppose you have the following list of values: 12, 13, 21, 27, 33, 34, 35, 37, 40, 40, 41. You could make a frequency distribution table showing how many tens, twenties, thirties, and forties you have:
Frequency |
Frequency |
10 - 19 |
2 |
20 - 29 |
2 |
30 - 39 |
4 |
40 - 49 |
3 |
Content Continues Below
You could make a histogram, which is a bar-graph showing the number of occurrences, with the classes being numbers in the tens, twenties, thirties, and forties:

(The shading of the bars in a histogram isn't necessary, but it can be helpful by making the bars easier to see, especially if you can't use color to differentiate the bars.)
The downside of frequency distribution tables and histograms is that, while the frequency of each class is easy to see, the original data points have been lost. You can tell, for instance, that there must have been three listed values that were in the forties, but there is no way to tell from the table or from the histogram what those values might have been.
On the other hand, you could make a stem-and-leaf plot for the same data:
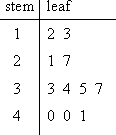
The "stem" is the left-hand column which contains the tens digits. The "leaves" are the lists in the right-hand column, showing all the ones digits for each of the tens, twenties, thirties, and forties. As you can see, the original values can still be determined; you can tell, from that bottom leaf, that the three values in the forties were 40, 40, and 41.
Note that the horizontal leaves in the stem-and-leaf plot correspond to the vertical bars in the histogram, and the leaves have lengths (in terms of numbers of entries) that equal the numbers in the "Frequency" column of the frequency table.
Content Continues Below
That's pretty much all there is to a stem-and-leaf plot. You're just listing out how many entries you have in certain classes of numbers, and what those entries are. Here are some more examples of stem-and-leaf plots, containing a few additional details.
-
Complete a stem-and-leaf plot for the following list of grades on a recent test:
73, 42, 67, 78, 99, 84, 91, 82, 86, 94
I'll use the tens digits as the stem values and the ones digits as the leaves. For convenience sake, I'll order the list, but this is not required:
42, 67, 73, 78, 82, 84, 86, 91, 94, 99
Since I know where these data points came from ("a recent test"), I'll use a title. Then my plot looks like this:

The above is the simplest case for stem-and-leaf plots, but even the "complicated" cases aren't much more complex.
URL: https://www.purplemath.com/modules/stemleaf.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()