Finding a Formula for a Parabola's Vertex
Purplemath
Since you always do exactly the same procedure each time you find the vertex form, the procedure can be done symbolically (using the algebraic quadratic y = ax2 + bx + c explicitly, instead of putting in numbers), so you end up with a formula that you can use instead of doing the completing-the-square process each time.
It's up to you, whether you want to memorize the formula for the coordinates of the parabola's vertex.
You'll probably be required to "show your work" in finding the vertex. Ask now if applying a memorized formula is acceptable. Either way, and particularly if you're expected to derive the formula yourself, here's how the formula deriviation goes:
- Derive the formula for the x-coordinate "h" of the vertex of any quadratic.
This is my generic quadratic equation.
y = ax2 + bx + c
My first step is to move the loose number (indicated by the contant c) over to the other side.
y − c = ax2 + bx
I factor out (that is, I pull out to the front) whatever is multiplied on the squared term.
Then I make room on the left-hand side for what will be added to both sides of the equation, and I put a copy of "a" in front of this space.
![adding extra space: y - a([space]) = a(x^2 + (b/a)x + [space])](square/vertex12a.png){kind=small}
I take half of the coefficient of the x-term (divide it by two) (and I mustn't forget its sign!); square this, and add it inside the parentheses on both sides.
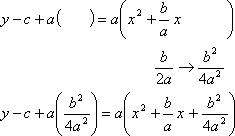
On the left-hand side, I multiply through the parentheses. The constant a cancels with one of the a's in the denominator.
I simplify on the left-hand side (by converting to common denominators, if necessary), and convert to completed-squared form on the right-hand side.
I move the loose numbers back over to the right-hand side.
I check the signs, and convert my equation to vertex form, as necessary. The "plus" in the middle of the first parenthetical is converted to "minus of a minus". To set things up for the second parenthetical, I've reversed the two terms, so the loose numbers can be combined following a "plus":
Then the the vertex (h, k) for any given quadratic y = ax2 + bx + c obeys the formula:
The original exercise asked only for the formula for the x-coordinate of the vertex, which is h. So my answer is:
Practically speaking, you can just memorize that and then plug your value for "h" back in to "y =" to calculate "k". If you're allowed to use this formula, you can then more quickly find the vertex, because simply calculating and then finding k is a lot faster than completing the square. On the other hand, even if you're not "supposed" to use this formula, you can still use it to check your work. If you're not sure if you completed the square correctly on a test, you can always use the formulaic answer to verify (or correct) whatever you've come up with.
However, if you've memorized the Quadratic Formula, you can probably easily memorize the formula here for k. The discriminant in the Quadratic Formula is b2 − 4ac. Take the negative of this to get the reverse of the subtraction:
−(b2 − 4ac) = 4ac − b2
The formula for h has a denominator of 2a; double this for a denominator of 4a. Put them together, and this gives you the formula for k.
© 2024 Purplemath, Inc. All right reserved. Web Design by 