Scalar & Matrix Multiplication
Purplemath
There are two types of multiplication for matrices: scalar multiplication and matrix multiplication.
What is scalar multiplication?
Scalar multiplication is the process of multiplying every entry in a matrix by the same number; this number is called the "scalar".
Content Continues Below
(The word "scalar" comes from the Latin "scalaris", related to the word for "ladder". A ladder can be used to "scale", or climb up and over, a wall. If you take linear algebra — after calculus — you may learn more about this.)
How do you multiply by a scalar?
Advertisement
Affiliate
To multiply a matrix by a scalar, multiply each entry of the matrix by the scalar's value. For instance, given a matrix M and the scalar −1, the scalar product −1M will multiply each entry in M by −1, so each entry in −1M will have the opposite sign of each entry in the original matrix M.
What are the properties of scalar multiplication?
The properties of scalar multiplication of a matrix are similar to the properties for multiplying numbers. Given a matrices X and Y and scalars c and d, we have the following:
- cX is a matrix
- cX = Xc
- c(dX) = (cd)X
- c(X + Y) = cX + cY
What is an example of multiplying by a scalar?
The following is an example of multiplying a matrix by a scalar.
- For the following matrix A, find 2A and −1A.
They've given me a matrix and two numbers; namely, the numbers 2 and −1. These two numbers are the scalars. So they're asking me to do scalar multiplication.
To do the first scalar multiplication to find 2A, I just multiply a 2 on every entry in the matrix.
Being excruciatingly complete, the process looks like this:
The other scalar multiplication, to find −1A, works the same way:
I can do the multiplications in my head, of course, but if an instructor wants to see every frickin' step, then I need to write things out like the above. You probably won't need to be this complete in your own work.
Having done the multiplications, my final answer (including which matrix goes with which multiplication) is:
You can use the Mathway widget below to practice multiplying a matrix by a scalar. (Or skip the widget and continue with the lesson.) Try the entered exercise, or type in your own exercise. Then click the button and select "Multiply" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Content Continues Below
Scalar multiplication is easy. Matrix multiplication, however, is quite another story. In fact, it's a royal pain in the hindquarters.
What is matrix multiplication?
Matrix multiplication is the process of multiplying one matrix by another matrix, when such multiplication is well-defined — that is, when the matrices fit the rule that make matrix multiplication work.
(We'll get to what that rule is on the next page.)
What is the formula for multiplying matrices?
Your textbook probably gave you a complex summation formula for the process of matrix multiplication, and that formula probably didn't make any sense at all to you. A typical statement of the formula is as follows:
Let A = αij be an s×m matrix, and let B = βij be an m×t matrix. Let AB = C = γij, where C is an s×t matrix.
Then, for 1 ≤ i ≤ s and 1 ≤ j ≤ t, the entries of C are defined as being:
...which is about as clear as mud.
That's okay. The process is messy, and that complicated formula is the best they can do for an explanation in a formal setting like a textbook. I'm way less formal, so I'll show you how the process really works:
- Find the product AB for the following matrices:
To calculate the product AB, I first write down A and B next to each other like this:
Now I need to multiply the entries in the ROWS of A by the entries in the COLUMNS of B. By this I mean that I take the first row of A and the first column of B, and I multiply the first entries of A's row and B's column, then the second entries of A's row and B's column, and then the third entries of A's row and B's column; and then I add the three products.
Affiliate
The sum of these three multiplications is one entry in the product matrix AB. In fact, being the product of row 1 and column 1, the summed result is the 1,1-entry of the product AB. Then I continue in like manner.
All the entries of the product matrix are found in this way. For instance, the sum of the products from row 2 of A and column 1 of B is the 2,1-entry of AB.
Which is all well and good, but what does this look like in practice?
What does matrix multiplication look like?
When I multiply matrices, I use my fingers to keep track of what I'm doing. The following animation is my attempt to illustrate this process. (Don't laugh; I'm no artist!)
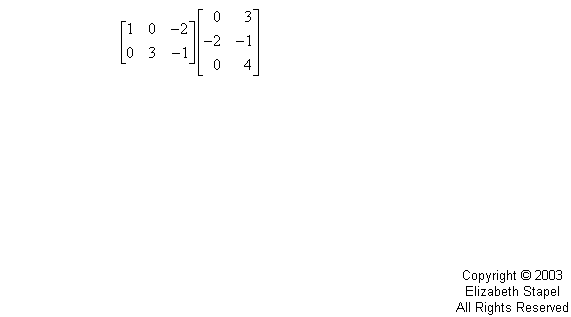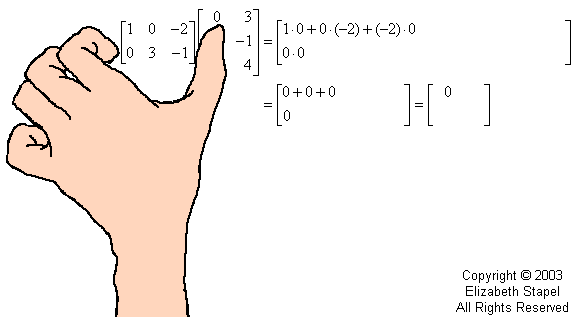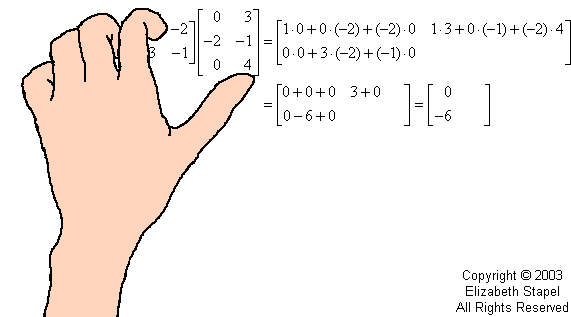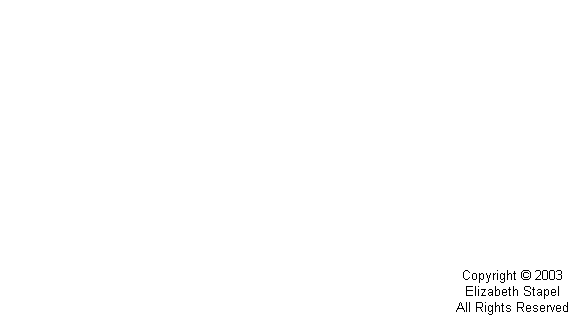
The above is an animated gif on the live website.
(Now, class; what did I say about laughing?) 😜
My final answer is:
To recap:
How do you multiply two matrices?
To multiply two matrices, you entry-wise multiply rows of the left-hand matrix by columns of the right-hand matrix. The sum of the products of the entries of the i-th row of the left-hand matrix and the j-th column of the right-hand matrix becomes the i,j-th entry of the product matrix.
This general rule is, in large part, what that complicated formula in your textbook was all about.
So when I, in the above animation, multiplied the first row (of A) and the second column (of B), this gave me the first-row-second-column entry in the product matrix AB.
URL: https://www.purplemath.com/modules/mtrxmult.htm
You can use the Mathway widget below to practice multiplying two matrices. (Or skip the widget and continue to the next page.) Try the entered exercise, or type in your own exercise. Then click the button to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




